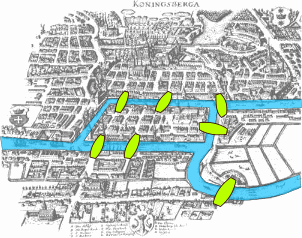
Königsberg’in yedi köprüsü; graf teorisinin temelini oluşturan ve XVIII. yüzyılda Königsberg köprülerinden ilhamlanılarak ortaya atılan ünlü bir matematik problemidir.

Königsberg kentinde Eski ve Yeni Pregel nehirleri birleşerek Pregel (Pregolya) nehrini oluşturmaktadır. Bu nehirler, şehri dört bölüme ayırmaktadır ve nehir üzerinde bu bölgeleri birleştiren yedi köprü bulunmaktadır.

Soru: Bütün köprülerden bir ve yalnız bir defa geçmek koşulu ile bir yürüyüş yapılabilir mi?

Bu soru, 1736’da İsviçreli matematikçi Leonhard Euler tarafından cevaplandırılmıştır.

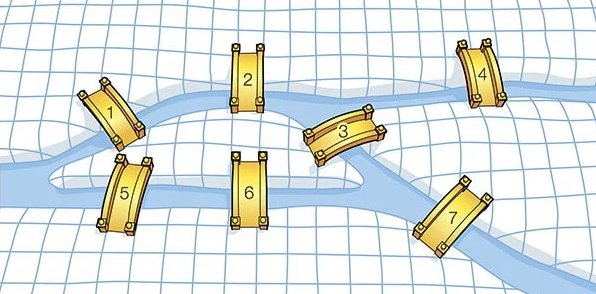
Basitçe,

Königsberg kentinde her köprüyü tam olarak bir kez geçerek dolaşmanın imkansız olduğunu gösteren Königsberg Köprüsü Probleminin çözümü, 1735’te Euler tarafından Petersburg Akademisi üyelerine sunuldu. Çözümü basitçe şu şekilde aktarabiliriz. Böyle bir yürüyüşü gerçekleştirmek isteyen kişinin iki seçeneği vardır. Seçeneklerinden ilki bir tur yapmaktır yani başladığı noktada yürüyüşünün bitirmektir. Diğer seçenek ise bir noktada yürüyüşe başlayıp başka bir yerde yürüyüşü tamamlamaktır. Önemli olan tek bir şey vardır. O da her köprüyü sadece bir kez geçmek. Aynı köprüden gidip geri dönmek bu nedenle mümkün değildir. Eğer ilk senaryodaki gibi bir yürüyüş yapar yani bir tur atarsanız yola çıktığınız kara parçasına bağlı en az iki köprü olması gerekir. Birini giderken diğerini de dönerken kullanacaksınız. Yani köprü sayısı çift olmalıdır. Grafik üzerinde düşünürsek de her daireye çift sayıda çizgi bağlı olmalıdır.

Farklı bir başlangıç ​​ve bitiş noktası olan ikinci senaryodaki gibi bir yürüyüşte, başlangıç ​​noktasında bir köprü ve bitiş noktasında bir köprü vardır. Yürüyüşünüz esnasında da bir köprüden kara parçasına ayak basar, diğer köprüden de çıkarak yolunuza devam ederseniz. Bu durumda eğer A noktasından B noktasına gidiyorsanız yola A noktasındaki köprüden geçerek çıkmalı sonra bir giriş bir çıkış iki ucu olan bir kara parçasından geçmeli ve son olarak bir köprü ile B noktasında varmalısınız. Şimdi yukarıdaki grafiğe göz atın. Her ada parçasına bağlı tek sayıda çizgi olduğunu göreceksiniz. İşte bu nedenle Königsberg şehrinin içinde her köprüden bir kere geçerek dolaşmak imkansızdır. Euler bu düşüncesini elbette biraz daha karmaşık biçimde dile getirdi. İki veya daha fazla düğüm içeren ( düğüm= daire) tüm graflar için geçerli kuralı şu şekilde belirledi. Her kenardan ( çizgiden) sadece bir kez geçen bir Euler yolu iki biçimde mümkündür. İlki tek dereceli ( derece: Daireden çıkan çizgi sayısı) tam olarak iki düğümün bulunmasıdır. Diğer düğümler de çift dereceli olmalıdır. Burada başlangıç noktası tek dereceli düğümlerden biri, bitiş noktası da tek dereceli düğümlerden diğeri olmalıdır. İkinci durumda da tüm düğümler çift dereceli olmalıdır. Bu durumda Euler yolu başladığı noktada bitecektir.

Euler’in çözümü

Euler çözümünde kara parçalarını harflerle, köprüleri ise sayılarla işaretlemiştir. Çözümü kolaylaştırmak ve şekli daha sade hale getirmek amacıyla kara parçalarının noktalarla, köprülerin ise çizgilerle temsil edildiği ikinci bir şekil yani graf (çizge) çizilir. Graflar graf elemanı, noktalar düğüm, düğüme bağlı olan elemanların sayısı ise düğüm derecesi olarak adlandırılmak üzere soru, grafın herhangi bir düğümünden başlayarak yedi elemanının her birini bir ve yalnız bir kere kullanarak dolaşma problemine dönüşmüş olur. Bu grafta A, B ve D düğümlerinin derecesi 3, C düğümünün derecesi ise 5’tir.

1736’da Euler’in incelemeleri böyle bir gezintinin mümkün olmadığını kanıtlamış ve bu tür dolaşmayı mümkün kılacak grafların şu özelliklere sahip olmaları gerektiğini göstermiştir: Birleşik bir grafın bütün elemanlarını bir ve yalnız bir defa kullanarak dolaşmak için o grafın tek dereceli düğümlerinin sayısı eğer varsa iki olmalıdır. Tek dereceli düğümler dolaşmanın başlangıç ve bitiş düğümleridir. Grafta böyle düğümler yoksa dolaşmaya herhangi bir düğümden başlanabilir.

Çözümün temelinde yatan düşünce şudur: Bir düğüm, başlangıç ya da bitiş düğümü değilse o düğüme gelen kişinin turu tamamlayabilmek için oradan ayrılması gerekecektir. Dolayısıyla bu tip düğümler çift dereceleri olmalıdır. Oysa tek dereceli bir düğüme, örneğin D düğümüne ikinci kez gelen bir kişi çıkış yolu bulamayacaktır. Dolayısıyla bu düğüm ya gezintinin bitiş düğümü olmalıdır ya da başlangıç düğümü olarak seçilmelidir ki ikinci gelişte çıkış yolu bulunabilsin. Buna göre tek dereceli düğüm sayısı ikiden fazlaysa gezinti tamamlanamayacaktır.

Yürüyüşün sonunda başlangıç noktasına dönülebilmesi içinse bütün düğümler çift dereceli olmalıdır. Böylece, başlangıç ve bitiş düğümü aynı olan ve her bir elemanı sedece ve en az bir kez içeren turlara “Euler turu” ve Euler turu içeren graflara da “Euler grafları” denmiştir.

Çözümün Kullanım Alanları

Ayrıt rotalama problemleri, pek çok araştırmacının üzerinde çalıştığı bir rota en iyilemesi problemidir. Bu problemin, gerçek hayatta mektup dağıtımı, yol bakımı, kar temizleme, çöp toplama, devriye araçları ve yol tuzlama konularında pek çok uygulaması vardır. Gerek hükümetler gerekse de işletmeler her yıl bu işlemler için önemli harcamalar yapmaktadırlar. Fakat planlamanın etkin olarak yapılamaması durumunda önemli miktarlarda kaynak israfı söz konusudur.